안녕하세요. 학생

Poisson Distribution은 쉽게 이야기하면 특정한 단위 시간동안(For example, per week, or per day)에 기존의 Event가 만들어 낸 Mean(즉, 평균)을 알고 있는 상황에서

다음 기간동안 그 Event가 특정한 횟수만큼 일어난 확률에 대한 분포를 나타내는 Distribution을 말합니다.

예를 들면 아주 오래전부터 지난주까지 학생의 집 앞 도로에서 "매 주 평균적으로" 교통사고가 2번씩 일어났다고 해봅시다.

이 사실을 학생이 알고 있을때...

그렇다면 다음주 월요일부터 일요일까지 한주 동안 그 도로에서 사고가 1번만 일어날 확률은 얼마일까? 또는 사고가 한번도 안 일어나거나 또는 사고가 3번 일어날 확률은 얼마일까?

이런 Probability Distribution을 의미합니다.

일반적으로 이 때 교통사고가 일어나는 사건을 X, 매주 일어나는 교통사고의 수 평균을 m=2로 놓고

X~Po(m=2)로 표시하고 그 다음 주에 특정 횟수 x만큼 사고가 일어날 확률 p(x)를 다음과 같이 계산하는 것으로 약속합니다. (붉은 색 부분)

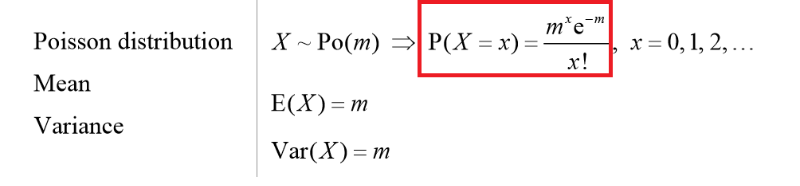
위의 교통사고의 예를 들면, 지금까지 교통사고의 횟수가 2번이었다는 것을 알때

다음주에 교통사고가 3번 일어날 확률은 m에 2를 대입하고 x에 3을 대입하면 됩니다. e는 natural constant 입니다.

위의 Formulae들은 시험시 Data book에서 제시하므로 외울 필요는 없습니다.

도움이 되길 바랍니다.